MAPA MENTAL SEGUNDO PERIODO

FUNCIONES LINEALES

   

Biografia de Pitagoras y Tales de Mileto

PITAGORAS

(Isla de Samos, actual Grecia, h. 572 a.C. - Metaponto, hoy desaparecida, actual Italia, h. 497 a.C.) Filósofo y matemático griego. Aunque su nombre se halla vinculado al teorema de Pitágoras y la escuela por él fundada dio un importante impulso al desarrollo de las matemáticas en la antigua Grecia, la relevancia de Pitágoras alcanza también el ámbito de la historia de las ideas: su pensamiento, teñido todavía del misticismo y del esoterismo de las antiguas religiones mistéricas y orientales, inauguró una serie de temas y motivos que, a través de Platón, dejarían una profunda impronta en la tradición occidental.

https://www.biografiasyvidas.com/biografia/p/pitagoras.htm

TALES DE MILETO 

(Mileto, actual Turquía, 624 a.C. - 548 a.C.) Filósofo y matemático griego. Iniciador de la escuela de Mileto, la primera de las escuelas filosóficas de la antigua Grecia, es considerado el primer filósofo por su aspiración a establecer una explicación racional de los fenómenos de la naturaleza, trascendiendo el tradicional enfoque mitológico que había caracterizado la cultura griega arcaica. Tales fue el primero que sostuvo la existencia de un arjé, es decir, de un principio constitutivo y originario común a todas las cosas, que identificó con el agua; inauguró con ello un tema recurrente en la filosofía presocrática y de vastas implicaciones en la tradición filosófica occidental.

https://www.biografiasyvidas.com/biografia/t/tales.htm

DESIGUALDADES E IN ECUACIONES DE PRIMER GRADO

DESIGUALDADES E IN ECUACIONES DE PRIMER GRADO

NECUACIONES DE PRIMER GRADO

Hemos visto ecuaciones de 1º y 2º grados, en los cuales el número de soluciones era siempre finito, o sea, una solución, dos soluciones. En este tema veremos un concepto nuevo, el de inecuación, el cual consiste en hallar los valores que cumplan una cierta expresión (desigualdad) matemática. En este caso, por regla general el número de soluciones será infinito.
Ecuación: 2x = 10 ; x = 5 como podemos comprobar la solución es única.
DEFINIENDO.-Una inecuación es una desigualdad en la que aparecen números y letras, llamadas incógnitas. ¿Para qué valores de x es cierto que ... < ... (Miembro de la izquierda es menor que el de la derecha? Las respuestas a esta pregunta es el conjunto solución de la inecuación. CONJUNTO SOLUCION.- Es el conjunto de valores de la incógnita que reemplazados en la inecuación, verifican la desigualdad. la solución de una inecuación generalmente se presenta por medio de INTERVALOS

Propiedades de las desigualdades:

1ª) Si se suma un número a los dos miembros de una desigualdad, se obtiene una desigualdad del mismo sentido que la primera (equivalente a la primera).
2ª) Si se multiplican o dividen los dos miembros de una desigualdad por un mismo número positivo, la desigualdad que resulta no varía su sentido. En cambio si el número es negativo, cambia el sentido de la desigualdad

http://matematicahumbertoluna.blogspot.com/2010/05/desigualdades-e-inecuaciones-de-primer.html

ECUACIONES DE PRIMER GRADO

ECUACIONES DE PRIMER GRADO

Resolver una ecuación consiste en encontrar el valor que debe tomar la incógnita $x$ para que se cumpla la igualdad. Podemos comprobar si la solución encontrada es correcta sustituyendo la incógnita $x$ por la solución. Como regla general, una ecuación de primer grado tiene una única solución. No obstante, puede darse el caso de que no exista ninguna o que existan infinitas (veremos algún ejemplo de estos casos).

Enlace: Ejercicios interactivos de álgebra básica

Ecuación 1

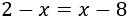
Solución

Para resolver la ecuación, debemos pasar los monomios que tienen la incógnita a una lado de la igualdad y los que no tienen la incógnita al otro lado.
Como 8 está restando en la derecha, pasa sumando al lado izquierdo:

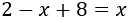Como $x$ está restando en la izquierda, pasa restando a la derecha:

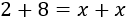Ahora que ya tenemos separados los monomios con y sin la incógnita, podemos sumarlos. En la izquierda, sumamos $2+8$ y, en la derecha, $x+x$:

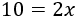Para ver con claridad el paso siguiente, escribimos $2x$ como un producto:

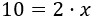Para terminar, debemos pasar el coeficiente de la incógnita (el número 2 que multiplica a $x$) al lado izquierdo. Como el número 2 está multiplicando, pasa dividiendo:

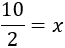Simplificando la fracción,

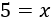Por tanto, la solución de la ecuación es $x=5$. Para comprobar la solución, sustituimos $x$ por 5 en la ecuación:

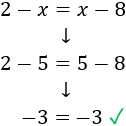Como hemos obtenido una igualdad verdadera (-3 es igual a -3), la solución es correcta. Si, por el contrario obtenemos una igualdad falsa, significa que hemos cometido algún error en la resolución de la ecuación.


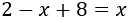
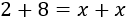
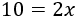
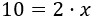
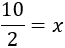
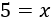
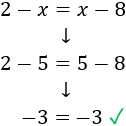
https://www.problemasyecuaciones.com/Ecuaciones/primer-grado/ecuaciones-primer-grado-resueltas-fracciones-parentesis-solucion.html

PROPIEDADES DE LA LOGARITMACION

PROPIEDADES DE LA LOGARITMACION

.1- Logaritmo de la unidad

El logaritmo de 1 en cualquier base es igual a 0.

log_b (1) = 0 ;  con b ≠ 1.

Ej:  log₅ (1) = 0    porque     5⁰ =1

log₇ (1) = 0   porque   7⁰ = 1

log₂₀ 1 = 0   ⇔  20⁰ = 1

2.2- Logaritmos de la base

El logaritmo de la base es igual a 1.

log_b (b) = 1 ; con b ≠ 1.

Ej:

log₅ (5) = 1  ⇔ 5¹ = 5

log₆ (6) = 1  ⇔ 6¹ = 6

log₁₂ (12) = 1  ⇔ 12¹ = 12

2.3- Logaritmo de una potencia con igual base:

El logaritmo de una potencia de un número es igual al producto entre el exponente de la potencia y el logaritmo del número.

log_b bⁿ = n,  con b ≠ 1

Ej:

log₆ 6 ³ = 3

2.4- Logaritmo de un producto

El logaritmo de un producto es igual a la suma de los logaritmos de los factores.

log_b (a • c) = log_b a + log_b  c

Ej:

log_b (5 • 2) = log_b 5 + log_b 2

2.5- Logaritmos de un cociente

El logaritmo de un cociente es igual al logaritmo del dividendo, menos el logaritmo del divisor.

Ej:

2.6- Logaritmo de una potencia

El logaritmo de una potencia es igual al exponente multiplicado por el logaritmo de la base.

log_a cⁿ = n log_a c 

Ej:

log₃ 10 ²  =  2 log₃ 10

2.7- Logaritmo de una raíz

El logaritmo de una raíz es igual al logaritmo de la cantidad subradical dividido entre el índice de la raíz.

Ej:

2.8- Cambio de base

 para todo p, a, b > 0;  b, c ≠ 1

https://www.portaleducativo.net/segundo-medio/35/logaritmos-propiedades

LOGARITMACION

LOGARITMACION

En análisis matemático, usualmente, el logaritmo de un número real positivo —en una base de logaritmo determinada— es el exponente al cual hay que elevar la base para obtener dicho número. Por ejemplo, el logaritmo en base 10 de 1000 es 3, porque 1000 es igual a 10 a la potencia 3: 1000 = 10³ = 10×10×10.

De la misma manera que la operación opuesta de la suma es la resta y la de la multiplicación la división, el cálculo de logaritmos es la operación inversa a la exponenciación de la base del logaritmo.

Para representar la operación de logaritmo en una determinada base se escribe la abreviatura log y como subíndice la base y después el número resultante del que deseamos hallar el logaritmo. Por ejemplo, 3⁵=243 luego log₃243=5. Cuando se sobreentiende la base, se puede omitir.

Los logaritmos fueron introducidos por John Napier a principios del siglo XVII como un medio de simplificación de los cálculos. Estos fueron prontamente adoptados por científicos, ingenieros, banqueros y otros para realizar operaciones fácil y rápidamente, usando reglas de cálculo y tablas de logaritmos. Estos dispositivos se basan en el hecho más importante —por identidades logarítmicas— que el logaritmo de un producto es la suma de los logaritmos de los factores:

https://es.wikipedia.org/wiki/Logaritmo

RADICACION

RADICACION

Radicación es el proceso y el resultado de radicar. Este verbo, por su parte, se refiere a lo que dispone de arraigo en un determinado lugar. Por ejemplo: “La radicación de la empresa en el polo industrial debe hacerse en la Secretaría de Producción”, “Los hechos muestran que la radicación en suelo australiano no fue una buena idea para la familia González”, “Tenemos que luchar contra la radicación de esos hábitos nocivos en nuestra comunidad”.

https://definicion.de/radicacion/